Competència matemàtica

• Comprensió dels diferents tipus de números i les seues operacions.
• Utilització de diversos contextos per a la construcció de nous coneixements matemàtics.
• Desenrotllar raonaments i construcció de conceptes.
• Identificació dels distints elements matemàtics que s'amaguen en un problema.
• Comunicació dels resultats de l'activitat matemàtica.
• Utilització dels coneixements i les destreses pròpies de l'àrea en les situacions que ho requerisquen.

Activitats Galeria d'Art

1. A una habitació rectangular, on situaries una càmera prequè fóra més eficient? Tindries suficient amb una?
A una de les cantonades. Amb una seria suficient per què es podria visualitzar tota l'habitació

2. I a aquestes habitacions?

A aquesta amb una a qualsevol cantó seria suficient per vigilar l'habitació sensera.

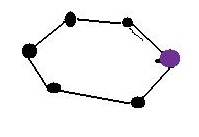
Imaginem que a aquesta habitació solament hi ha un punt pintat de lila, per lo tant hi ha soles una càmera (m'hen engañat amb el dibuix). Amb una sola càmera situada a un cantó hi hauria suficient visivilitat com per a vigilar tota l'habitació

A aquesta habitació amb una càmara situada des del punt lila podriem vigilar la resta. Es convex.

3. Aquestes habitacions són convexes. Un polígon és convex si una línia recta que uneix dos punts situats dins del polígon no es pot eixir fora del polígon.
Per tant, quantes càmeres necessitem si l'habitació és convexa?
Amb una càmera és suficient.

4. En realitat, les galeries d'art necessiten molta paret llisa disponible per a penjar quadres, i una manera d'aconseguir-ho és utilitzar polígons no convexos (o còncaus)

5. Pot aquesta sala ser vigilada per tres càmeres situades als punts B, C i E?
Si, amb eixes cameres als 3 punts es vigilaria tota la sala.
Trobaries alguna manera de vigilar-la només amb dues càmeres?
Desde els dos punts que hi ha entre el C i B i el D i E.

6. Quin és el mínim nombre de càmeres per a vigilar aquestes dues sales? Marca els vèrtexs on les situaries.
Les tres senyalades

UNIFORMES. A favor o en contra?

Uniformes, es poden vore a escoles, treballs i dictadures. Afavoreix l'uniforme? Fa que siguem més amics? Ens fa millors persones? Jo pense que no, solament trobe argunments en contra d'anar tots iguals. I si jo vull portar el mueu propi estil?

L'uniforme es impossat sense tindre en compter l'opinió dels que tenen que portar-ho. Si ara decideixen impossar uniforme al meu institut, no em queda altra opció que possarmelo encara que no vuiga.

Jo no estic a favor de l'uniforme escolar, tal vegada alguns beneficis siguen identificar-nos entre una escola i altra, però, i si per exemple jo no vull que la gent sàpiga que estudie al Figueras? O també, no tindre que preocupar-me de que em posse.

No anem a ser millors o més importants per portar uniform i a més és una falta de llibertat d'expressió.

Uniform procedeix de:

UNI: Del llatí, un, tots iguals

FORM: De forma. 

Tots de la mateixa forma.

No vull anar com tots, no vull formar part d'un mateix exèrcit o ramat, per aixó dic NO a l'uniforme.

LA OLA

La Ola és la pel.lícula que hem estat veïent en Atenció Educativa. Tracta d'un mestre que treballa a un institut d'Alemania. A aquest mestre li manen fer unes classes, que duren una setmana, sobre l'autocràcia.
La primera pregunta que fa a els seus alumnes el primer dia es, si pensen que podria haver a Alemania altra dictadura con la que va impossar Hitler al 1932. Com és d'esperar, els seus alumnes li responen que no, que seria totalment imposible així que el mestre anomenat Rainer decideix comprovar-ho per si mateix.
El primer dia els fa alçarse per a parlar i quan ell entra a l'aula.
El segon dia els fa que tots es possen una samarreta blanca i al llarg dels dies fa cosses com aquestes.
Es dona el cas de que una alumna no vol possar-se samarreta blanca i els demés de la classe l'aïllen; en canvi, a un altre company que sempre havia estat marginat se l'acepta com un altre qualsevol.
Al llarg de la setmana es va comprovant que el grup format per Rainer, anomenat ''La Ola'', es fa com una pinya, es defenen entre ells, intenten tindre més membres al seu grup e inclús als que no ho són els marginen i no els traten gaire bé.
Aquest experiment de Rainer s'en va de les mans i encara que aconsegueix para al grup i demostra-los lo que en realitat succeïa recordant-los la pregunta del primer dia, acava en trajedia.

El problema de la galeria d'art.

Aquest problema de geometria computacional, enganyosament senzill, va ser proposat inicialment al 1973 per el geòmetre i topòleg Victor Klee.
Suponguem que tenint el plà de la planta d'una galeria es desitja saber quants guàrdies es necesiten colocar per a que tot punt de la galeria estiga continuament vigilat. De manera equivalent es poden imaginar llums en compter de guàrdies i així requerim ilimunació completa.
El problema es pot definir formalment com:
-Donat un polígon simple de n costats, determinar el mínim nombre de vèrtex des de els que es possible vore tots els punts interiors del polígon.
Per a un polígon simple amb n costats, (n/3) guardies son a vegades necessaris i sempre suficients per a vigilar un polígon. Aquests guardies poden sempre colocarse als vèrtex del polígon.

Circumcentre d'un triàngle

El circumcentre d'un triangle és el centre de la circumferència circumscrita al triangle, per lo que la distància a cada un dels seus vèrtex és la mateixa(radi). En concret, és el punt d' intersecció de les mediatrius del triangle(sent una madiatriu la recta penpendicular a un costat que passa per el punt mitjà del mateix). Per lo tant, per a representar gràficament el circumcentre, dibuixarem les tres mediatrius i localitzem el punt d'intercecsió de les mateixes.

Videos de la triangulació de Delaunay

Alguns videos sobre la triangulació de Delaunay:

Relació amb els diagrames de Voronoi

Una triangulació de Delaunay poseix la caracteristica de ser el graf dual al diagrama de Voronoi. Per a cada triangle, el centre del cercle circunscrit per el triangle, correspon un vertex generador del diagrama de Voronoi i les perpendiculars als costats del triangle formen les arestes del diagrama de Voronoi.
Per lo tant, es pot construir la triangulació de Delaunay a partir del diagrama de Voronoi, unint tots els generadors que compartisquen un eix de Voronoi, i unint aquells punts veïns en regions de Voronoi obertes.
Propietats del dos diagrames:
◘La triangulació de Delaunay es un grafi de linies rectes duals al diagrama de Voronoi
◘Cada triangle de Delaunay poseeix com vértex als generadors del diagrama de Voronoi
◘La triangulació de Delaunay y el diagrama de Voronoi tenen el mateix nombre de arestes y es corresponen entre si. Cada aresta de la triangulació es perpendicular a una aresta de Voronoi.
◘La frontera de la triangulació de Delaunay es la envolvent convexa dels punts.
◘Una triangulació és de Delaunay si tots els cercles que passen per tres vértex de un triangle son buits. Per lo tant, no es possible trobar cap punt del núvol a l'interior dels triàngles formats per la triangulació , es a dir, l'interior de cada triangle no poseix generadors